Henshin/Examples/ProbabilisticBroadcast

The Probabilistic Broadcast example illustrates state space analysis of so-called probabilistic graph transformation systems modeled in Henshin. We model here a probabilistic broadcast protocol for wireless sensor networks.

A detailed description of the approach and the example can be found in this paper: Christian Krause, Holger Giese: Probabilistic Graph Transformation Systems. Proc. of ICGT'12, Lecture Notes in Computer Science 7562, Springer-Verlag. The slides for this paper are available here.

The transformation rules, topology models and the source code can be found here. To run the Java executable you need Henshin 0.9.3 or higher and PRISM 4.0 or higher.

Modeling

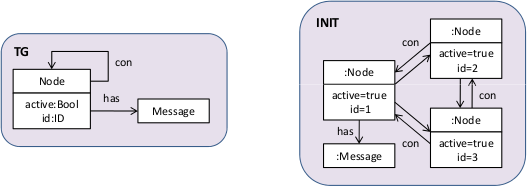
The figure below depicts the metamodel (type graph) and an example of an instance model. The metamodel consists of two classes: Node and Message. A node can be connected to an unbounded number of nodes (its neighbors) and can contain an unbounded number of messages. The example instance model on the right-hand side consists of three connected nodes (all connections are bidirectional). One of these nodes has a message, the others not. All of the nodes are active.

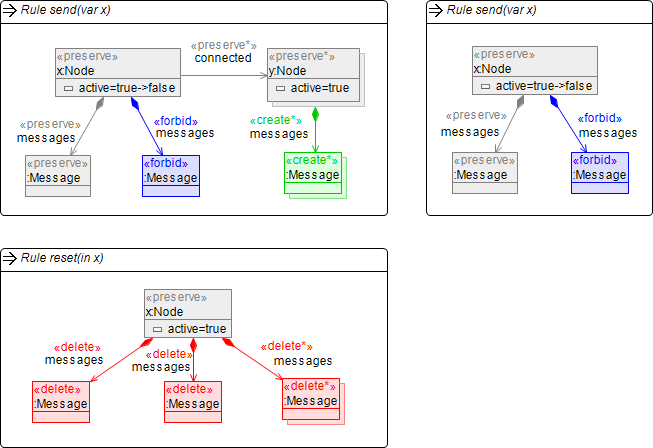
The goal of the probabilistic broadcasting is to send the message to all nodes in the network. The sending of messages is possible only to direct neighbors of a node. Moreover, if a node receives a message from more than one neighbor, it is interpreted as a collision and the node considers the message as corrupt. The idea of probabilistic broadcasting is that every node decides with a certain probability whether to forward its message or not. This lowers the chance of message collisions and reduces the general communication costs. We model the probabilistic broadcasting using three rules in Henshin shown below.

There are two rules called send. The one on the left adds messages to all neighbors of a node that has exactly one message (remember that more than one message per node are considered as collisions). The second send rule also matches a node with exactly one message, but it does not forward the message to its neighbors. Note that in both send rules, the active-status of the node x changes from true to false. The rationale for having these two rules with the same name is that the sending of the message is decided probabilistically. That means, the two rules are formally considered as one probabilistic rule which consists of one LHS and two RHSs (modeled in the two send rules). If matched, the left send rule is executed with a probability pSend and the right send rule with a probability of 1-pSend. The third rule allows a node to reset itself by deleting all its messages whenever a collision occurred (it has more than one message).

Evaluation

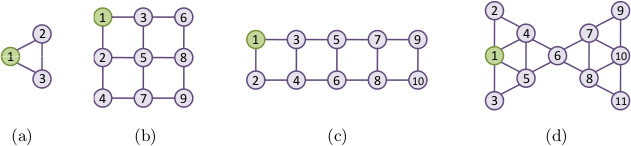
Based on the theory presented in the ICGT paper, we evaluated the modeled system to determine the probabilities of the reception of a message by the nodes in a network. We analyzed the protocol for 4 different network topologies shown in the image below. In each of these networks, node 1 is the one that initiates the broadcasting. Network (a) is the one shown in abstract syntax in the previous section.

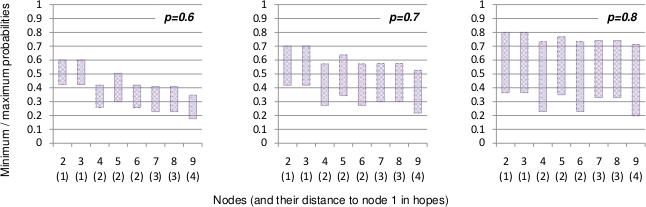
The figure below shows the minimum and the maximum probabilities for each node in network (b) correctly receiving the message and for send probabilities of pSend=0.6, 0.7 and 0.8. The minimum probabilities represent worst-case, the maximum probabilities best-case message sending orders for each node. Note that the minimum (and the maximum) probabilities for the different nodes vary more or less depending on the chosen send probability and the location of the node in the grid.

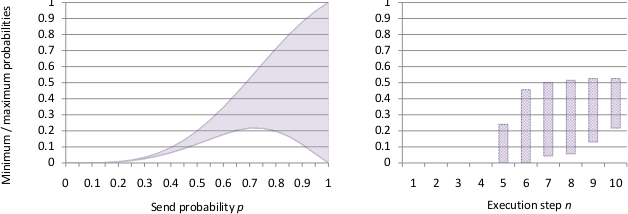
To show the impact of the send probability, we have plotted the minimum and the maximum reception probabilities for node 9 with changing values for the send probability. The results are shown in the left-hand side of the figure below. Note that for send probabilities greater than approx. 0.7, the minimum reception probability decreases again. The diagram on the right-hand side shows how the reception probability increases for a node 9 in network (b) after 1..10 execution steps.

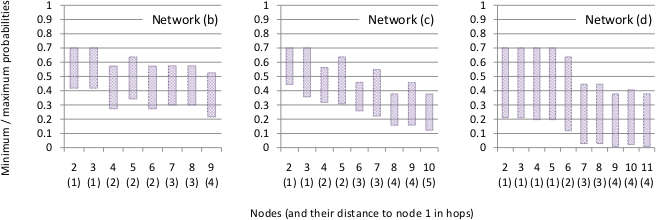
In our last experiment, we compared the reception probabilities for the different network topologies (see figure below). The reception probabilities drop more for the nodes in network (c) with high indizes than in network (b) which is caused by the higher distance and the fewer number of connections. For network (d), the differences between the minimum and maximum probabilities are higher than in the other networks. This is caused by the higher connectivity of the network which increases the chance for collisions. It is also evident that node 6 is a bottleneck in the network causing the probabilities to drop abruptly for nodes 7-11.

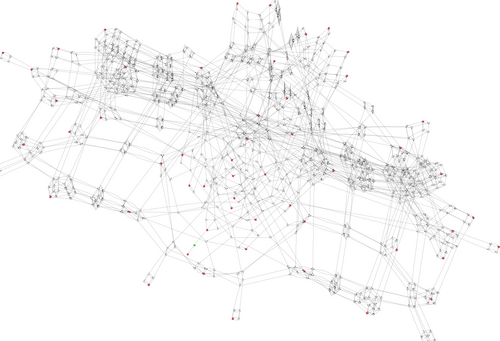
All conducted analysis is based on the state space generation support in Henshin. The figure below shows a visualization of the state space for network (b) (state space visualized using the Henshin Statespace Explorer).

contributed by Christian Krause