VIATRA2/Mutual Exclusion Benchmark

Outdated page

This page contains obsolete information about the VPM based VIATRA2 and preserved for archive purposes only.
The currently maintained wiki is available at http://wiki.eclipse.org/VIATRA

Mutual exclusion (A Varró benchmark)

Benchmark description

The Varró benchmark suite defines a set of transformations on which many transformation systems have been measured. One part of this benchmark suite is based on a distributed mutual exclusion algorithm. This section will introduce the implementation of the library of graph transformation rules that make up the benchmark. Furthermore, the transformation machines are also given that implement the long transformation sequence (LTS) and short transformation sequence (STS) algorithms outlined in the benchmark suite. Finally, some measurements are presented.

The mutual exclusion test case describes a process ring arbitrating control of resources. After growing the process ring to the required size, the STS version creates one resource that is owned by one process; in the next phase, every process issues a request on that resource; the resource will be passed along the ring until a full cycle is performed. LTS starts with a complete ring and a separate resource owned by every process; the whole set of resources is shifted along the process ring once in each cycle, involving waiting and blocked processes, as well as a deadlock-resolving algorithm. The ring size is the characteristic parameter in both cases; for LTS, the number of executed cycles can also be specified.

For a detailed test specification, see the following article:

Varró G., Schürr, A., Varró D.: Benchmarking for graph transformation. In: Proc. IEEE
Symposium on Visual Languages and Human-Centric Computing (VL/HCC 05), Dallas,
Texas, USA, IEEE Press (September 2005) 79–88

Or visit this page: Varró Gergely: Graph transformation benchmarks

Metamodeling

Metamodel of the mutual exclusion problem set

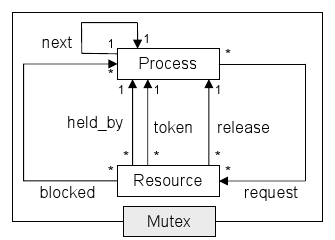
First, we have to build the metamodel of the benchmark set. Processes and resources will be represented as Viatra entities, and their associations as relations; they will all be contained in the mutex.metamodel namespace. The following VTML file describes the metamodel (for the sake of simplicity, we have not asserted any multiplicity constraints):

entity(mutex)
{
  entity(metamodel) {
    entity(resource);
    entity(process);
    relation(next, process, process);	
    relation(blocked, resource, process);
    relation(held_by, resource, process);
    relation(token, resource, process);
    relation(release, resource, process);
    relation(request, process, resource);
  }		
}

We create a new Viatra model space for this benchmark by the new VIATRA2 VPM model space wizard (accessible at File/New/Other ). Opening the model space will display the Tree Editor, which can be used to directly manipulate the model space. The Eclipse view titled "VIATRA2 Models spaces" will also show a new line representing the opened model space; loading the metamodel into our new model space is as simple as drag&dropping the .vtml file from the Package Explorer (or Project Explorer) onto this item.

TODO link VTML files?

Initial model

Initial model of the mutual exclusion problem set (particularly STS)

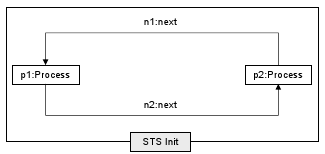
Now we have our metamodel, but the initial model (see figure) still needs to be constructed. There are several ways to achieve this.

Programmatic construction: the machine executing the transformation (or a separate VTCL machine) can create the initial model itself (before starting the benchmark timer). For example, the following code could be inserted at the beginning of the main() sequence:

//initialisation
let Model = undef, N1 = undef, N2 = undef, P1 = undef, P2 = undef in seq {
  new (entity(Model) in mutex);
  rename(Model, "model");
  new (mutex.metamodel.process(P1) in mutex.model);
  new (mutex.metamodel.process(P2) in mutex.model);
  new (mutex.metamodel.process.next(N1, P2, P1));
  new (mutex.metamodel.process.next(N2, P1, P2));
}

Note that N1, N2, P1, P2 are merely variable names and the created entities and relations receive generated names; if the need arises to name them properly, use rename().

Manual creation: the VIATRA2 Model Editor (the aforementioned tree editor) can be used to create the model. Navigate to the entity representing the namespace mutex and select "Add Entity" from the context menu. A new entity will appear as a child of mutex, alongside metamodel. Select "Rename" from the context menu of this entity to name it "model". We now have the mutex.model namespace. Next, we use the tree editor to create two child entites; the Eclipse view titled "Properties" allows us to specify mutex.metamodel.process as the "Type" of these entities (and possibly to rename them). By selecting "Add Relation" from the context menu of each process, we add a self-referencing relation to each of them. The new relations appear as a child node of the respective entities, as if they were contained by their source element; this is in conformance with the rule governing their fully qualified name. As a consequence, dragging and dropping each relation onto the other entity would change their source element, which is just what we need. Using the "Properties" view again, these relations can be typed ; their source and target could also have been specified here.

Import model: the initial model can be represented in VTML and imported via drag&drop just as easily as the metamodel.

namespace mutex;
  entity(model) {
    mutex.metamodel.process(p1);
    mutex.metamodel.process(p2);
    mutex.metamodel.process.next(n1, p2, p1);
    mutex.metamodel.process.next(n2, p1, p2);
  }

Note that the namespace mutex has already been created; this VTML file merely references it. Also, the model elements are properly named now, conforming to the figure shown above. This method seems to be the smoothest, so we'll apply this one.

TODO link VTML files?

Pattern and rule library

During the development of the benchmark implementation, multiple versions of the transformation were developed (STS versus LTS; gtrules versus patterns and rules; debug versus "release" version). However, they all share the common set of graph transformation rules defined in the benchmark description. To avoid the needless replication of the transformation rules, all patterns and rules have been isolated into single VTCL machine (mutex.lib). This machine contains no main() rule, it is therefore not executable; it merely serves as a shared library. The different executable transformation machines all reference patterns and rules defined in this library.

The graphical representation of the "releaseRule" transformation rule

The benchmark consists of a great number of transformation rules. Here we only present the implementation of a single representative, namely releaseRule.

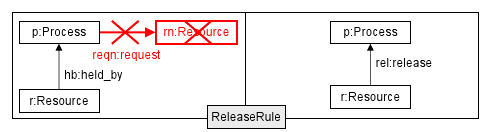
Writing a VTCL code that embodies this transformation rule consists of two steps: first, create a graph pattern according to the LHS (left-hand-side) of the transformation rule; second, implement the action sequence that is to be executed on finding that pattern (i.e. transforming LHS into RHS). Before we can construct the LHS pattern, there is an obstacle to overcome: it contains a negative application condition (NAC). Occurrences shall be rejected if the process still has an unfulfilled request for a resource. So the NAC can be formulated as a pattern that matches those processes that do have an outgoing edge of type "request" to a resource; the availability of this pattern will block our LHS pattern. In VTCL, this is coded as a pattern on processes, see below:

pattern req(P) = {
  process(P);
  resource(Rn);
  process.request(Reqn, P, Rn);
}

Now we can incorporate this NAC into the LHS pattern. The LHS is a pattern consisting of a process (that does not match the NAC), a resource, and a held-by relation between them, as shown below:

pattern releaseRule_lhs(P, R, HB) = 
{
  process(P);
  resource(R);			
  resource.held_by(HB, R, P);
  neg pattern req(P) = {
    process(P);
    resource(Rn);
    process.request(Reqn, P, Rn);
  }
}

Finally, we write the simple rule sequence that manipulates the model:

rule releaseRule(in P, in R, in HB, out Rel) = seq
{
  delete(HB);
  new(resource.release(Rel, R, P));	
}

There is an option that resembles the graph rule formalism more closely: the gtrule construct. Although the version above will be used for its greater flexibility, we still present an alternate way to express the same thing in VTCL:

gtrule releaseRule_gtrule(out P, out R) = 
{
  precondition find releaseRule_lhs(P, R, HB);			
  postcondition pattern rhs(P, R, HB) = 
  {
    process(P);
    resource(R);
    resource.release(Rel, R, P);
  }		
}

Here the right-hand side is also presented in a graph pattern format. The variable HB is not present in the RHS, even though it's listed as one of its symbolic parameters; this is the way to express deletion. Variables that are not symbolic parameters of the postcondition will not be deleted. Note that we simply reused the pattern releaseRule_lhs for the precondition; alternatively, it could have been defined locally just as the RHS. Or alternatively, we could reuse the RHS as an action sequence as well (which could be even simpler if it weren't for the output parameter Rel):

gtrule releaseRule_gtrule(out P, out R) = 
{
  precondition find releaseRule_lhs(P, R, HB);			
  action { 
    let Rel = undef in call releaseRule(P, R, HB, Rel); 
  }	
}

After writing the VTCL code for the other transformation rules, our mutex library will look like this:

namespace mutex;
import mutex.metamodel;
 
//@incremental
machine lib
{
// [...]	
  pattern releaseRule_lhs(P, R, HB) = 
  {
    process(P);
    resource(R);			
    resource.held_by(HB, R, P);
    neg pattern req(P) = {
      process(P);
      resource(Rn);
      process.request(Reqn, P, Rn);
    }
  }	
  rule releaseRule(in P, in R, in HB, out Rel) = seq
  {
    delete(HB);
    new(resource.release(Rel, R, P));	
  }		
// [...]
}

By drag&dropping this .vtcl file onto the opened model space (in the VIATRA2 Modes spaces view), we can parse this library into the VIATRA2 framework. Another option is pressing Ctrl+P, if the file is open in a VTCL editor. Both options require that the model space already contains the metamodel. By uncommenting the annotation above the machine, the incremental pattern matcher will be used instead of the default one.

STS machine

The short transformation sequence of parameter Size consists of the following steps:

1. newRule is applied Size-2 times to enlarge a ring
2. mountRule is applied once to create a single resource attached to one of the processes
3. requestRule is applied on each LHS occurrence so that all processes file a request on the resource
4. an as-long-as-possible cycle consisting of single applications of takeRule, releaseRule and giveRule so that each process acquires the resource for a short time and then hands it over to the next one

First, let's see how to apply a rule once. The following construct selects one occurrence or a LHS pattern:

choose P1, P2, N with find mutex.lib.newRule_lhs(P1, P2, N) do [...something]

The omitted part can use the bound pattern variables arbitrarily. Now we'll use them to execute the model manipulation rule. Ideally, this would look like the following:

choose P1, P2, N with find mutex.lib.newRule_lhs(P1, P2, N) do 
    call mutex.lib.newRule(P1, P2, N);

However, our implementation of newRule, much like releaseRule above, also has some output variables to return the value of the newly created elements (that can be printed for debugging purposes, etc.). Therefore these output variables need to be declared in the caller scope too:

choose P1, P2, N with find mutex.lib.newRule_lhs(P1, P2, N) do 
  let P = undef, N1 = undef, N2 = undef in 
    call mutex.lib.newRule(P1, P2, N, P, N1, N2);

The iterate construct of VTCL executes an action repeatedly until it fails. To create a simple cycle that applies newRule Size-2 times, we write an iterated action that fails if the desired number of iterations have been reached, and otherwise applies the rule as above. Step 1 is implemented this way:

// step1: new processes
let StepCount = 0 in iterate 
  if(StepCount < Size-2) seq
  {
    update StepCount = StepCount+1;
 
    choose P1, P2, N with find mutex.lib.newRule_lhs(P1, P2, N) do 
      let P = undef, N1 = undef, N2 = undef in
        call mutex.lib.newRule(P1, P2, N, P, N1, N2);
  } else fail;
//println("step 1 done");

The body of the let/in construct can be replaced with a sequence block that, besides calling the rule itself, updates counters or other tracking data and/or prints useful debug information about the execution of the rule and the newly created elements, etc.

Step 2 is a simple rule application, it does not deserve special mention. Before discussing Step 3, let's see Step 4:

 
// step4	
iterate seq{
  choose P, R, T, Req with find mutex.lib.takeRule_lhs(P, R, T, Req) do 
    let HB = undef in call mutex.lib.takeRule(P, R, T, Req, HB);
  choose P, R, HB with find mutex.lib.releaseRule_lhs(P, R, HB) do 
    let Rel = undef in call mutex.lib.releaseRule(P, R, HB, Rel);
  choose P1, P2, R, Rel with find mutex.lib.giveRule_lhs(P1, P2, R, Rel) do 
    let T = undef in call mutex.lib.giveRule(P2, R, Rel, T);								
};
//println("step 4 done");

It uses the same iterate construct, meaning that it tries to execute this three-rule cycle as long as possible, stopping on first failure (which occurs when all rules have already been fulfilled).

Step 3 could use the iterate construct too, but it uses the forall construct instead, meaning that all occurences of the LHS are determined in one step, and then the rule is executed on each one of them. In some cases, this may lead to different behaviour; now it was chosen solely for performance considerations, as it only needs a single pattern matching query.

 
// step3
forall P, R with find mutex.lib.requestRule_lhs(P, R) do 
  let Req = undef in call mutex.lib.requestRule(P, R, Req);		
//println("step 3 done");

Measurement results

The measurements have been carried out on a standard desktop computer with a 2 GHz Intel Core2 processor, 2 gigabytes of system RAM available, the Windows Vista operating system, running version 1.6.0 05 of the 32-bit Sun Java SE Runtime (for VIATRA2) and version 3.0 of the .NET Framework (for GrGEN.NET). In general, several test runs were executed, ranging from five to ten runs on different test cases. The transformation sequences were coded so that little or no output was generated; in the case of VIATRA2, the GUI was not disabled. Execution times were measured with millisecond precision as allowed by the operating system calls.

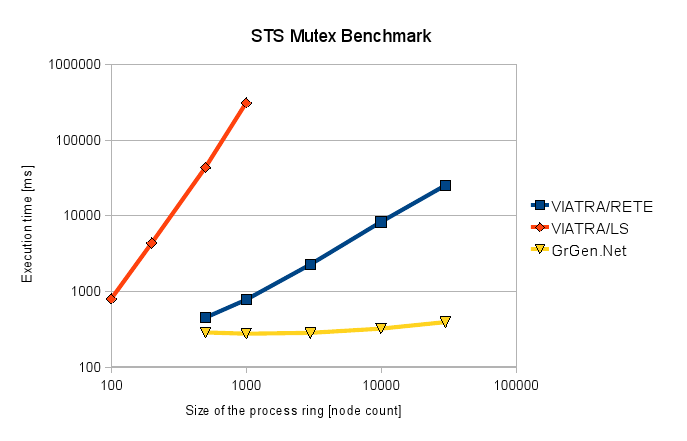
In order to compare the pattern matcher algorithms using an already available benchmark, the performance of the VIATRA 2 local search based (VIATRA/LS) and incremental (VIATRA/RETE) pattern matchers have been evaluated along with GrGEN.NET (considered to be one of the fastest graph transformation systems) with the short transformation sequence version of the distributed mutual exclusion algorithm test set, which is not a primary application field for incremental pattern matching.

The results show that the incremental approach is more efficient than the default pattern matcher implementation (local search), since the current unoptimized local search algorithm cannot operate in linear time. Nevertheless, VIATRA2 is still outperformed by the highly optimized GrGen.NET.