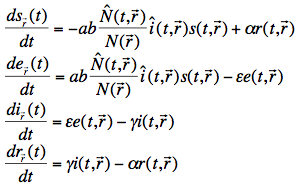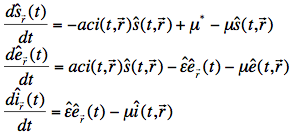Notice: This Wiki is now read only and edits are no longer possible. Please see: https://gitlab.eclipse.org/eclipsefdn/helpdesk/-/wikis/Wiki-shutdown-plan for the plan.
MacDonald Ross Disease Model
Malaria
Our model for malaria transmission is based on work originally carried out by Ross (1911) and MacDonald (1957). The cycle of the malaria and its transmission between secondary human hosts and primary vectors of the genus Anopheles is complex. It suffices to say that a human infection begins when sporozoites are injected by an infected female mosquito into the blood stream. The sporozoites migrate to the liver, and after some period of time they enter the bloodstream in the form of gametocytes which can be injected into a mosquito when it ingests human blood. Through a series of development within the mosquito, the injected gametocytes becomes gametes which (in the sexual phase) turns into a zygote, then a motile ookinete which bores through the gut of the mosquito and releases a large number of sporozoites. This completes the cycle.
Our model can be described by a set of differential equations describing the dynamics of the disease in both the human and the Anopheles vector. From the description of the malaria cycle above, it is clear that we need to model some period of latency from the time of the blood meal to the infectious stage in both human and vector. For humans, the latent period is defined as the time from initial infection to the appearance of gametocytes in the blood. For the Anopheles vector, the latent period is defined as the time from initial infection to the appearance of sporozoites in the mosquito saliva glands (also called sporogonic cycle). Once the Anopheles mosquito is infectious, it is assumed to stay infectious for the rest of its life. Humans, on the other hand, are able to clear gametocytes from the blood stream over time and do not stay infectious indefinitely. Once recovered from an infection, a human has built up antibodies against the parasite. However, antibodies decay over time and long periods of no exposure tend to result in lowered antibody titres within individuals.
The set of differential equations determining the state of a human population for a single region r is defined as:
where (leaving out the region) s(t), e(t), i(t) and r(t) are the relative number of susceptible, exposed, infectious and recovered humans, a is the biting rate on humans by a single mosquito (defined as the number of bites per unit of time), b is the fraction of infectious bites on humans that produces an infection, ![]() is the total number of mosquitoes at time t (from our Anopheles model described earlier), N is the total number of humans (assumed constant over time),
is the total number of mosquitoes at time t (from our Anopheles model described earlier), N is the total number of humans (assumed constant over time), ![]() is the relative number of infectious mosquitoes,
is the relative number of infectious mosquitoes, ![]() is the immunity loss rate,
is the immunity loss rate, ![]() is the human latent period and
is the human latent period and ![]() is the rate at which humans recover from an infection.
is the rate at which humans recover from an infection.
The corresponding set of differential equations for the Anopheles mosquito population has fewer variables (since the mosquitoes never recover from an infection):
where (again leaving out the region), ![]() ,
, ![]() and
and ![]() are the relative number of susceptible, exposed and infectious mosquitoes, a is the biting rate (same as above), c is the fraction of bites by susceptible mosquitoes on infected people that produces an infection,
are the relative number of susceptible, exposed and infectious mosquitoes, a is the biting rate (same as above), c is the fraction of bites by susceptible mosquitoes on infected people that produces an infection, ![]() is the latent period for the mosquito,
is the latent period for the mosquito, ![]() is the background mosquito birth rate and
is the background mosquito birth rate and ![]() is the background mosquito death rate.
is the background mosquito death rate.
The background mosquito birth rate (![]() ) and death rate (
) and death rate (![]() ) deserve further explanation. The Anopheles model we described earlier determines the number of female mosquitoes in a region at any given time
) deserve further explanation. The Anopheles model we described earlier determines the number of female mosquitoes in a region at any given time ![]() .
. ![]() depends on the four environmental factors as well as the human population density, and varies over time. However, when
depends on the four environmental factors as well as the human population density, and varies over time. However, when ![]() remains constant, the background birth rate and death rate is for the mosquito is assumed the same (
remains constant, the background birth rate and death rate is for the mosquito is assumed the same ( ![]() =
= ![]() ) and it is described by a single parameter of the model. When the mosquito population is growing, we simply increase the birth rate
) and it is described by a single parameter of the model. When the mosquito population is growing, we simply increase the birth rate ![]() to reflect the growth. When the population is shrinking, we reduce the birth rate. In some cases however, the mosquito population is shrinking so rapidly that setting the birth rate to zero is not enough. When this happens, we increase the death rate
to reflect the growth. When the population is shrinking, we reduce the birth rate. In some cases however, the mosquito population is shrinking so rapidly that setting the birth rate to zero is not enough. When this happens, we increase the death rate ![]() to keep up with the drop in the mosquito population.
to keep up with the drop in the mosquito population.
Ross R (1911) The prevention of malaria (2nd ed.). Murray, London
Macdonald G (1957) The epidemiology and control of malaria. Oxford University Press, London