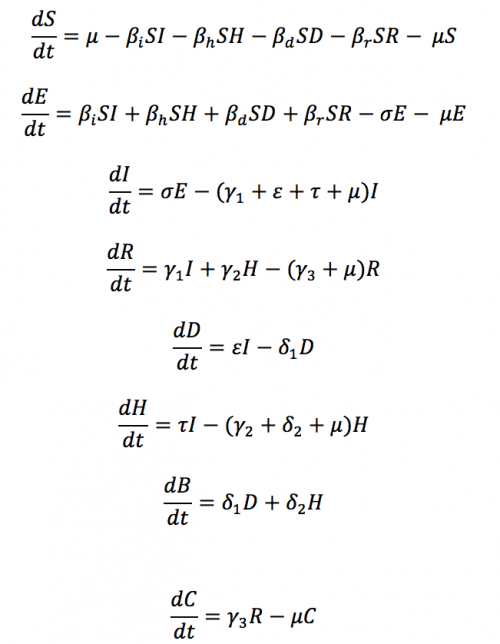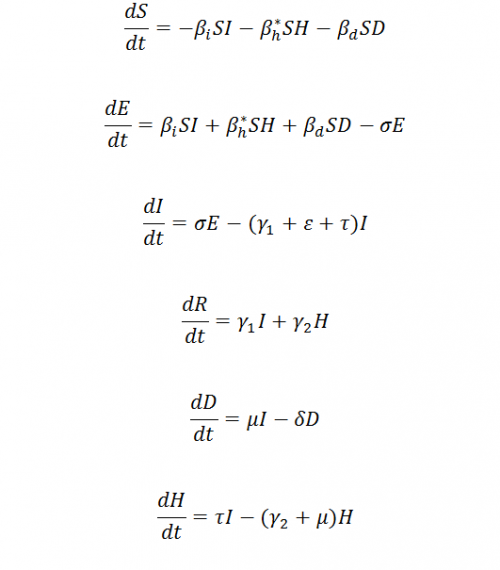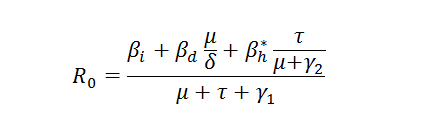Notice: This Wiki is now read only and edits are no longer possible. Please see: https://gitlab.eclipse.org/eclipsefdn/helpdesk/-/wikis/Wiki-shutdown-plan for the plan.
Ebola Models
This page describes models for Ebola available on this site. The official Eclipse Ebola model is not the only Ebola model available, nor is the first one that was created using STEM. Please also see the following page of Ebola References (including additional Models from the literature)
Outbreak Background
The current Ebola outbreak in West African countries may have been triggered by an initial infection in Dec 2013. The first case was thought to be a 2 years old patient lived in a village in Guinea [REF]. This patient, who showed the typical symptoms of the disease (i.e., fever, black stool and vomiting), died on Dec 6 2013. [Ref] A chain of illnesses in patient zero’s family has been found and several family members have caught the infection and died thereafter. While attending the funeral, it is believed that two attendees brought back the virus to their village because funeral tends to bring people in close contact with the body. Contact between mourners and the deceased is a social practice for many African communities and represents and important contact pathway for disease transmission. Clusters of the disease appeared in early 2014 in Guinea, Liberia and Sierra Leone. Ebola Virus Disease (EVD), formerly known as Ebola hemorrhagic fever (EHF) is a fatal illness in humans. Ebola is caused by infection with a virus of the family Filoviridae, genus Ebolavirus. The virus spreads through direct contact with infected blood or body fluids (i.e., urine, saliva, feces, vomit, and semen), contaminated objects (e.g., needles) and infected animals. According to WHO, men who have recovered from the disease can still transmit the virus through their semen for up to 7 weeks after recovery from illness. The incubation period generally ranges between 2 to 21 days (WHO). Symptomatic infection lasts about 10 days. The case fatality rate can be as high as 90%. No specific vaccine or medicine (e.g., antiviral drug) has been proven to be effective against Ebola.
Available Eclipse/STEM Ebola Model
The model described below is a preliminary model the STEM developers are contributing to help researchers get started with their own models. It can easily be extended and as we learn more about the current virus (and as that virus mutates) more sophisticated models will no doubt follow. In particular a future model should separate populations into different demographic groups - those whose practices involve contact with deceased people, and those that do not. The current models uses only one "standard" population so that behaviors is captured only in an average way (that does not vary from country to country). The model below is optimized for the three countries in Africa currently most affected by the epidemic (Guinea, Sierra Leon, Liberia).
Using STEM’s automated model building tool (see Figure 1), we have implemented a preliminary epidemiological model for Ebola based on 8 compartments and 8 differential equations. The code is automatically generated by STEM's model builder and transparent to any user. For more information on the model builder please see the STEM Model Creator page and | this YouTube tutorial.
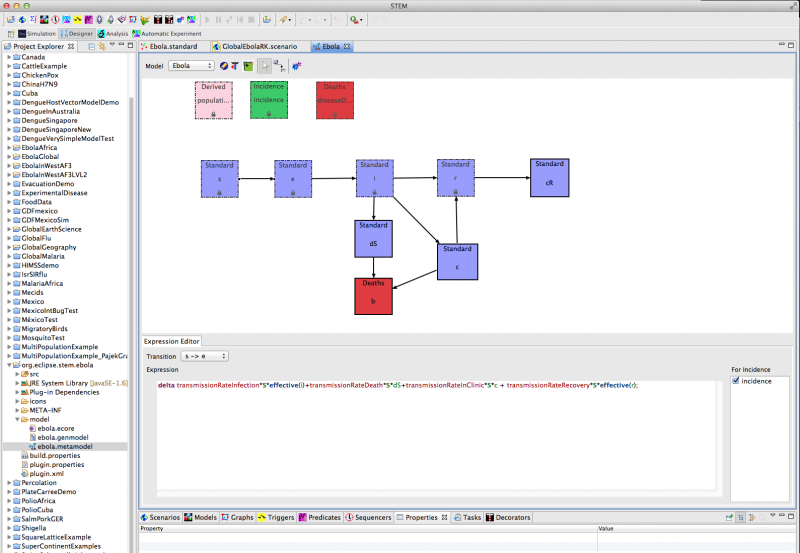 Figure 1: Creating a new model for Ebola using the STEM model builder tool
Figure 1: Creating a new model for Ebola using the STEM model builder tool
The design of the model is shown in Figure 2. It includes the usual Susceptible, Exposed, Infectious, states along with 5 additional compartments: death (but not buried), buried, clinical isolation, and burial (B). The usual R compartment in this model does NOT mean recovered or removed. In this case R represents asymptomatic but still infectious as an STD. WHO indicates transmission, β_r, is still possible for seven weeks after symptoms have gone away through semen by sexual activities among partners. We modeled this post-symptomatic infectious state (R) to capture the possibility of this 7-week of limited transmission. Researchers who question this infection pathway can simple zero out this transmission rate.
Complete recovery is represented by the C compartment. Regarding compartment B, significant infection is believed to happen due to post-mortem contacts with an infectious corpse from the disease, at home or during funeral. This transmission pathway of Ebola is also captured in the model.
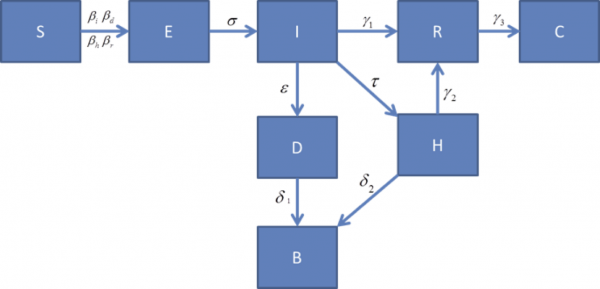 Figure 2: Compartment Model for Ebola
Figure 2: Compartment Model for Ebola
Model Equations
The differential equations defining the model shown in Figure 2 are listed below. If you download the Ebola scenario the terms that build up to form these differential equations are shown in the Model Builder's equation editor - just click on each transition to see the terms. The generated code can be selected in the project explorer (LHS of figure 1).
Differential equations defining the compartment model shown in figure 2'
The model above also includes clinical isolation in a clinic or hospital (Compartment H) and can be tuned to capture breakdown of infection control (infection between healthcare workers and infected patients).
When sexual transmission of Ebola is not the focal point of study at this moment, we remove R compartment in Figure 2 which turns off the sexual transmission. The collection of equations becomes:
Basic Reproductive Number
The basic reproductive number, Ro, is defined as the number of secondary infections caused by one primary infection introduced to a fully susceptible population at a demographic steady state (Anderson and May, 1991; MacDonald, 1957; MacDonald, 1965). From the differential equations above, when we turn off the sexual transmission which is not the focal transmission pathway to consider for now, we derive analytically the expression of Ro.
The Basic Reproductive Number for Ebola depends on several infection pathways.
Effect of Zoonotic Reintroduction
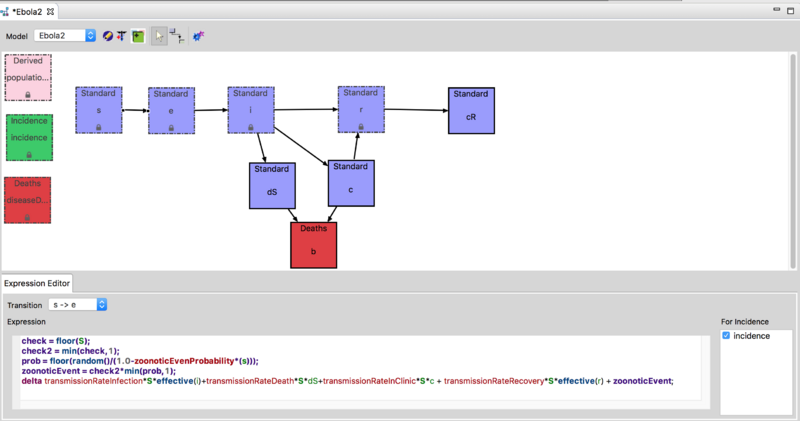
Using the model builder the basic Ebola Model was extended to support a study of the effect of quasi-periodic (stochastic) zoonotic reintroduction of Ebola into a community. The expression editor window in the figure below shows how the infection process was modified to include a stochastic term representing random introduction from a zoonotic reservoir. This model is available on the downloads page. For more information on how to run the model please see the Ebola Zoonotic Reservoir Documentation.
In this extended model, the effect of the disease reintroduction from the reservoir is described by a new proportionality term, k*S, added to the susceptible class. The parameter k indicates the rate of infection of a susceptible individual by contact with an infected animal in the wild (reservoir).
The net effect of k also scales with the population specified separately in the initializer for the human population model. This can be customized in by editing the initializer located in the STEM decorator folder (see EbolaSingleNode/decorators/HumanPopInitializerSingleNode.standard).
The value of k does not modify the value of R0, but rather makes the probability of stochastic initiation of an epidemic following an extinction event non zero. For realistic values of the parameter k, the disease dynamics between reintroduction events is, on average, described by the Ebola model without reservoir (see above). Hence, R0 is not modified by K (ref to paper in press).
Explicitly modeling the reservoir allows for investigation of the fragility of target populations under continuous disease pressure, and the potential for establishing an endemic state.
The value of k estimated for West Africa is k = 5x10-9 /person/day.
Third-Party Ebola Models
Operon Labs Ebola Models
To our knowledge the first STEM Ebola model for the 2014 outbreak was created by former NIH scientist Alexander J. Jones (Operon Labs) in early September 2014. The model is slightly different from the one available Eclipse, but it's still very informative. The Operon Labs model is based on a STEM Standard (built in) SEIR Compartment model. All model parameters have been updated as of Oct 22 2014. You can comment on the model in the forum
The Operon Labs Ebola models are under active development. The versions released on Oct 22nd 2014 are known as the "C3" versions. The Operon Labs Ebola models have used two sources of Ebola disease parameters. . .
Operon Labs Ebola Model version C3
- The latest Operon Labs 'C3' Ebola Outbreak Model SEIR parameters are as follows (derived from the NEJM/WHO data):
- 1/σ (Incubation Period) : 9.4 days (Single-day Exposures, All Countries, Observed)
- 1/γ (Infectivity Period): 8.2 days (Derived from Observed Serial Interval (All Countries) - Incubation Period) (17.6 Days - 9.4 Days)=8.2 days
- σ (Incubation Rate, STEM) : 1 / 9.4 days = 0.1063830
- γ (Infectivity Rate) : 1 / 8.2 days = 0.12195120
- f (Case Fatality Rate): 0.708 (NEJM/WHO)
- γ_STEM: Recovery Rate (STEM): (1-f)*γ = 0.292*γ = 0.03560976
- δ_STEM Mortality Rate (STEM): f*γ = 0.708γ = 0.0863414496
- R0 (Reproduction Num#) : 1.84 ( Weighted Avg, All Countries)
- βstem(Transmission Rate) = R0 * γ
- βstem(Transmission Rate) = 1.84 * 0.12195120
- βstem(Transmission Rate): = 0.224390208
- Experimental testing of the above parameters in West Africa and the United States with standard SEIR resulted in the following:
- Td_model (Model Doubling Time) = ~16.3 days (This number varies by country and exact section of curve)
- Td_actual (Actual Doubling Time) = 15.74 days (Weighted Average, Liberia+SL+Guinea)
- Serial Interval (Model Serial Interval) = Not Calculated
- Serial Interval (Actual Serial Interval) = 17.6 days (Used to derive the infectious period)
- These resulting parameters are very close to the actual behavior of the outbreak on the ground, in particular for West Africa. Quite usefully, all model parameters were derived from clinical data that was taken as weighted averages of all Ebola infected countries as of Sep 2014.
Disclaimer: The following is not a prediction by the Eclipse foundation or the STEM project developers. These are the values one should expect to see if one runs the built in SEIR model with the parameters listed above. At the current time Ebola cases are growing exponentially and this output is an example of exponential growth but does not reflect intervention efforts or other factors that could change the rate at which the virus is spreading.
- Output of the Operon Labs West African SEIR model with the parameters specifies as above should show the following...
- Date / I+R+D (Infected+Recovered+Dead) / Fatalities
- Oct 01 2014 / 7,281/ 3,819
- Oct 22 2014 / 22,224 / 14,734
- Nov 01 2014 / 34,699 / 22,535
- Dec 01 2014 / 125,922 / 84,914
- Jan 01 2015 / 425,554 / 291,847
- Feb 01 2015 / 1.3 million / 0.9 million
- Mar 01 2015 / 3.3 million / 2.4 million
- Apr 01 2015 / 6.6 million / 5.3 million
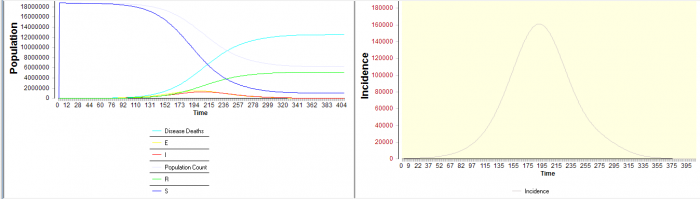
- Peak incidence in West Africa appears to occur in late-March 2015. . . The graph below starts in Sep 15 2014 with WHO seeded parameters in Guinea, Liberia, and Sierra Leone. (A corresponding outbreak in the USA takes about 14 to 15 months from disease import to peak incidence). These models assume no effective intervention occurs , and the virus stays at R0=1.84 throughout the outbreak.
- Operon Labs West Africa Simulation Results with Ebola 2014 Parameters