Notice: this Wiki will be going read only early in 2024 and edits will no longer be possible. Please see: https://gitlab.eclipse.org/eclipsefdn/helpdesk/-/wikis/Wiki-shutdown-plan for the plan.
Difference between revisions of "STEM Solvers"
| Line 12: | Line 12: | ||
y(t+h) = y(t) +h*y'(t) | y(t+h) = y(t) +h*y'(t) | ||
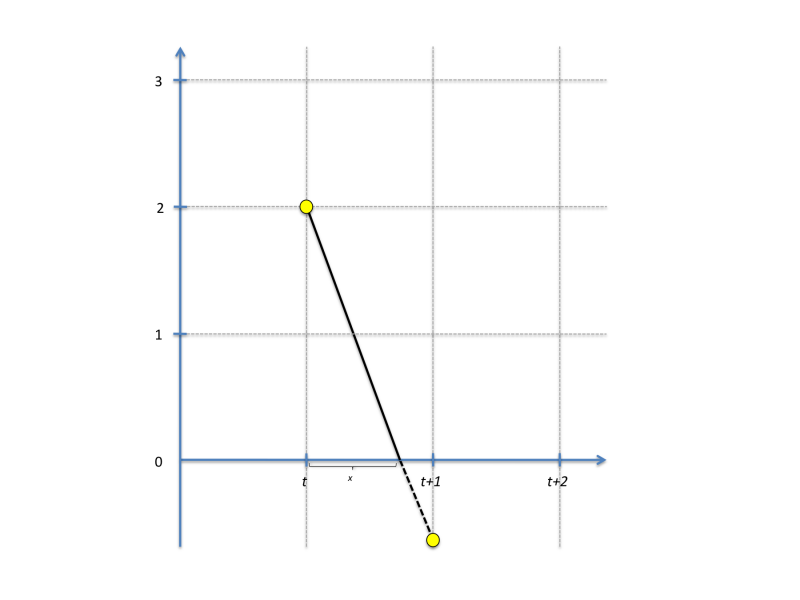
| − | where h is the step size (default 1 day in STEM as defined by the sequencer). Label values in STEM are often constrained to a positive value. For instance, the count of a population can never go negative, and this is also true for any population assigned to a particular compartment state. When a constrained value goes negative, the finite difference solvers | + | where h is the step size (default 1 day in STEM as defined by the sequencer). Label values in STEM are often constrained to a positive value. For instance, the count of a population can never go negative, and this is also true for any population assigned to a particular compartment state. When a constrained value goes negative, the finite difference solvers does a partial step to avoid this as illustrated in this figure: |
[[Image:FiniteDifferenceFigure.png|800px]] | [[Image:FiniteDifferenceFigure.png|800px]] | ||
| Line 20: | Line 20: | ||
y(t+h) = y(t) + x*y'(t)+(1-x)*y'(t+x) | y(t+h) = y(t) + x*y'(t)+(1-x)*y'(t+x) | ||
| − | The algorithm finds the smallest x among all differential equations solved and rescales all label values accordingly. The finite difference solver is able to take advance of multi-core CPUs and each CPU is assigned a sub-set of the graph to work on. | + | The algorithm finds the smallest x among all differential equations solved and rescales all label values accordingly. If necessary, multiple partial steps are carried out. |
| + | |||
| + | The finite difference solver is able to take advance of multi-core CPUs and each CPU is assigned a sub-set of the graph to work on. | ||
=== Runge Kutta Cash-Karp === | === Runge Kutta Cash-Karp === | ||
| + | The Runge Kutta Cash-Karp solver is an adaptive step size ordinary differential equation solver that calculates six function evaluations for each time step and estimates two solutions (of 4th and 5th order). The difference between the two solutions is the estimated error and the solver can be calibrated to any desired degree of accuracy. If the error exceeds the tolerance the step size is reduced. The Runge Kutta Cash-Karp solver can take advantage of multi-core CPUs and each CPU is assigned a sub-set of the graphs to work on. The CPUs synchronize the step size to ensure that the same solution is reached now matter how many CPUs are running concurrently. | ||
| + | |||
=== Dormand Prince === | === Dormand Prince === | ||
Revision as of 19:25, 16 January 2012
When you create a new scenario in STEM, you need to specify which solver to use. A solver is simply the method used to determine how the state of a simulation changes from one time step to the next. Models for populations and diseases in STEM are all designed to carry out this change or derivative calculation given a current state. How the derivative is applied to determine the next state is where solvers differ.
Available solvers
Finite Difference
The finite difference solver is the most straightforward (and fastest) solver available. It's using Euler's method and simply estimates the next value from the current value plus the derivative:
y(t+h) = y(t) +h*y'(t)
where h is the step size (default 1 day in STEM as defined by the sequencer). Label values in STEM are often constrained to a positive value. For instance, the count of a population can never go negative, and this is also true for any population assigned to a particular compartment state. When a constrained value goes negative, the finite difference solvers does a partial step to avoid this as illustrated in this figure:
(the figure assumes h = 1). The next value is thus calculated as:
y(t+h) = y(t) + x*y'(t)+(1-x)*y'(t+x)
The algorithm finds the smallest x among all differential equations solved and rescales all label values accordingly. If necessary, multiple partial steps are carried out.
The finite difference solver is able to take advance of multi-core CPUs and each CPU is assigned a sub-set of the graph to work on.
Runge Kutta Cash-Karp
The Runge Kutta Cash-Karp solver is an adaptive step size ordinary differential equation solver that calculates six function evaluations for each time step and estimates two solutions (of 4th and 5th order). The difference between the two solutions is the estimated error and the solver can be calibrated to any desired degree of accuracy. If the error exceeds the tolerance the step size is reduced. The Runge Kutta Cash-Karp solver can take advantage of multi-core CPUs and each CPU is assigned a sub-set of the graphs to work on. The CPUs synchronize the step size to ensure that the same solution is reached now matter how many CPUs are running concurrently.