Notice: this Wiki will be going read only early in 2024 and edits will no longer be possible. Please see: https://gitlab.eclipse.org/eclipsefdn/helpdesk/-/wikis/Wiki-shutdown-plan for the plan.
Difference between revisions of "Henshin/State Space Tools"
| Line 1: | Line 1: | ||
| − | + | To verify the correctness of transformations, Henshin provides a tool for | |
| + | generating and analyzing the state spaces of in-place model transformation. | ||
| + | To some extent this can be compared to a debugger: starting from some initial | ||
| + | state, the transformation is executed in a stepwise fashion and can be, thus, | ||
| + | analyzed, e.g. to make sure that all intermediate states are correct fulfill | ||
| + | some invariants. However, state space analysis is much more powerful than | ||
| + | debugging, because instead of inspecting one particular execution path, | ||
| + | the complete state space incuding all possible traces is generated. | ||
| + | It goes without saying that the state space should be finite for this | ||
| + | to work. However, abstraction techniques can be used to keep state spaces | ||
| + | finite and small. | ||
| − | + | == Features == | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[Image:Statespace-explorer-phil-win32.png|350px|right|x]] | |
| − | + | ||
| − | + | ||
| − | * ( | + | The state space tools in Henshin currently support the following features: |
| + | * Efficient (multi-threaded), resumable generation of explicit state spaces | ||
| + | * Various state-based abstractions (graph isomorphism, attribute and node ID abstraction) | ||
| + | * Visualization of small state spaces based on a spring layout algorithm | ||
| + | * Structural state invariant checking using OCL | ||
* Qualitative model checking using [http://www.inrialpes.fr/vasy/cadp CADP] and [http://www.mcrl2.org mCRL2] | * Qualitative model checking using [http://www.inrialpes.fr/vasy/cadp CADP] and [http://www.mcrl2.org mCRL2] | ||
| − | * Probabilistic model checking using [http://www.prismmodelchecker.org PRISM] | + | * Probabilistic model checking using [http://www.prismmodelchecker.org PRISM] |
| − | + | * Export to LaTeX, AUT, SM files | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | All these functionalities are integrated in Henshin's graphical state space explorer, shown on the right. However, they can be also invoked from the context menu for state space files or | ||
| + | programmatically. For model checking, the state space explorer provides a uniform front-end to the above mentioned analysis tools. | ||
= State Space Generation = | = State Space Generation = | ||
Revision as of 09:07, 2 February 2011
To verify the correctness of transformations, Henshin provides a tool for generating and analyzing the state spaces of in-place model transformation. To some extent this can be compared to a debugger: starting from some initial state, the transformation is executed in a stepwise fashion and can be, thus, analyzed, e.g. to make sure that all intermediate states are correct fulfill some invariants. However, state space analysis is much more powerful than debugging, because instead of inspecting one particular execution path, the complete state space incuding all possible traces is generated. It goes without saying that the state space should be finite for this to work. However, abstraction techniques can be used to keep state spaces finite and small.
Contents
Features
The state space tools in Henshin currently support the following features:
- Efficient (multi-threaded), resumable generation of explicit state spaces
- Various state-based abstractions (graph isomorphism, attribute and node ID abstraction)
- Visualization of small state spaces based on a spring layout algorithm
- Structural state invariant checking using OCL
- Qualitative model checking using CADP and mCRL2
- Probabilistic model checking using PRISM
- Export to LaTeX, AUT, SM files
All these functionalities are integrated in Henshin's graphical state space explorer, shown on the right. However, they can be also invoked from the context menu for state space files or programmatically. For model checking, the state space explorer provides a uniform front-end to the above mentioned analysis tools.
State Space Generation
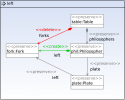
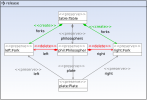
As a running example we consider the academic example of dining philosophers. To make it more interesting we include a rule for a dynamic reconfiguration, i.e. to allow to add a philosopher to the table during the execution. The rules are depicted below. We have two rules left and right for picking up forks, a rule release for putting them back on the table, and finally a rule create for squeezing in a new philosopher. We include negative application conditions to make sure that we cannot add arbitrarily many philosophers. This is important to ensure that the state space is finite. Here we chose an upper limit of at most 5 philosophers. We should also point out again that we can model both the execution and the reconfiguration using transformation rules in Henshin.
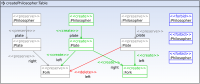
Now that we have defined our transformation rules, we need to create an initial configuration for our dining philosopher system. We choose an initial configuration of 3 philosophers where all forks are lying on the table. We can define this either using a generated EMF editor for the philosophers model, or the sample reflective editor. Make sure though that the Ecore modeled is regisetered in the EMF package registry.
Now we are all set and ready to generate our state space. Open the New wizard and select State space in the Henshin category. After finishing the wizard a new file with the extension statespace is created and opened in the graphical state space explorer.
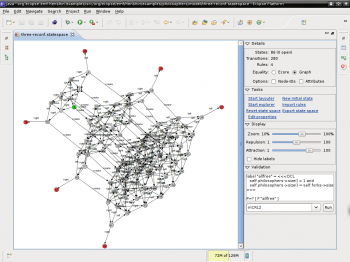
On the right-hand side you can find control panel for the explorer. On the top the number of states, transitions and rules is display. Here you can also find some switches which influence the state space generation:
- Equality: this can be either Ecore or Graph. By default this is set to graph and this is also the right choice for 95% percent of the cases. Using the graph equality the state space gets signifcantly smaller and yet is fully equivalent to the original one based on Ecore equality.
- Option node IDs: whether to ignore attributes when comparing two states. This is disabled by default. In the future we will enable it automatically if it is save to do so.
- Option attribute values: whether to ignore attributes when comparing two states. This is disabled by default. In the future we will enable it automatically if it is save to do so.
Now we need to 1) import rules to be used in the state space generation, and 2) load the initial philosophers model into the state space as an initial states. You can do both of them in the context menu of the explorer, as shown below.
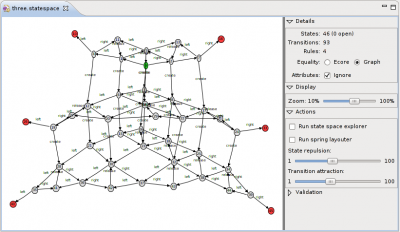
The initial state is now the staring point for building up the state space. You can explore or unfold a state by simply double clicking on it. This will create a number of follow-up states which are connected with the base state using transitions.
To enable automatic layouting, click on Run spring layouter in the Actions menu in the control panel.
We can continue to unfold states by double clicking on them. States are being colored in the explorer based on the following scheme:
- green: initial state
- grey: an explored state
- blue: an open state (one that can be explored by double clicking)
- red: deadlock or terminal states (no rules are applicable here)
You can also let the tool do the work for you: click on Run state space explorer to automatically build up the state space.
After a number of steps the state space for our philosophers examples is fully generated. It should look more or less like below.
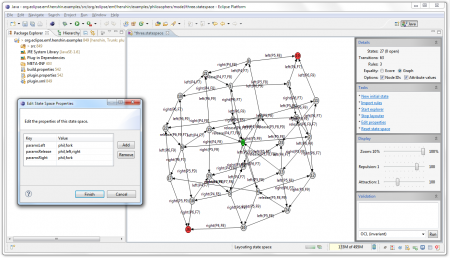
State space can be also generated outside of the graphical explorer. This is of course much more efficient. You can do this by clicking on Explore State Space in the State Space submenu in the context menu of statespace files. You can also click on Properties in the context menu of state space files to see some details about it. Note that statespace files have a binary format and can get rather large, depending on the size of the state space. The generator is currently able to handle state spaces with millions of states and tens of millions of transitions. You can open such big files also in the graphical explorer, but they will not be vizualized anymore.
Another often used functionality is to reset a state space. This removes all derived state space (all states which are not initial). You can do this also from the context menu.
Parameterized Actions
Validation
To validate a state space open it in the graphical explorer and make sure it is fully explored (it has no open states). Then you can use the Validation menu in the control panel to validate it.
OCL Invariants
You can specify OCL constraints in the validation tool in the explorer and check them for your state space. For example in the dining philosophers state space we can check the following constraint:
- self.forks->size()>0
meaning that there is always at least one fork on the table. After having selected OCL (invariant) in the drop down menu, we can simply click on Run to check the constraint. In out case this should give us a negative result. Moreover, a trace into a state which does not fullfil the constraint is automatically selected in the explorer. This gives you essentially a counterexample for your invariant.
Model checking with CADP and mCRL2
Full model checking of temporal properties is supported using external model checkers. For qualitative model checking you can currently use either CADP or mCRL2. To use the tools in Henshin you have to install it somewhere on your computer. Note that CADP requires an (academic) license, whereas mCRL2 is open source.
When you have installed either of the tools, make sure their ar in the system-wide PATH, so that Henshin can find them. For CADP you also have to define the environment variable CADP, which should point to the directory where it is installed.
Now you can model check your state space. Both mCRL2 and CADP support the model mu-calculus which has a great raw expressive power, but is also hard to read/write. You can check deadlocks in the mu-calculus using the formula:
- [true*] <true> true
This should evaluate to false in our example. CADP moreover generates a counterexample which is shown in the explorer (here a trace into one of the deadlock states).
Another property that we can check is the following:
- <true*>nu X.<left.right>X
which basically says: Is there an infinite sequence of the actions left and right? This should evaluate to false. However, if we try:
- <true*>nu X.<left.right.release>X
we should get a true. Note that in CADP you have to put quotes around the action names.
Probabilistic Analysis with PRISM
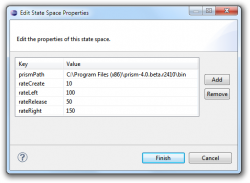
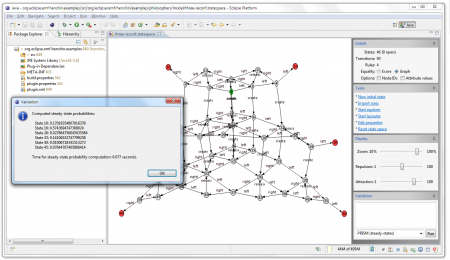
For a stochastic analysis of your transformation you can use the PRISM model checker. A standard task in PRISM is to compute so-called steady-state probabilities for a state space. With this you can essentially find out what the probability is for your system to be in a certain state.
To compute steady-state probailities in the Henshin explorer choose the tool PRISM (steady-states). You can just click on run. Now the tool will complain that you have to specify some rates. It generates a properties file for you which you can edit now to enter the rates. After having saved the properties file and clicking again on Run you should get the steady-state probabilities for your state space, as shown below.
If you have any questions please use the henshin-dev mailing list or contact me directly.