Notice: this Wiki will be going read only early in 2024 and edits will no longer be possible. Please see: https://gitlab.eclipse.org/eclipsefdn/helpdesk/-/wikis/Wiki-shutdown-plan for the plan.
Difference between revisions of "GEF3D Coordinate Systems"
m |
(added category GEF3D) |
||
| (13 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
== Coordinate Systems == | == Coordinate Systems == | ||
=== Mouse Coordinates === | === Mouse Coordinates === | ||
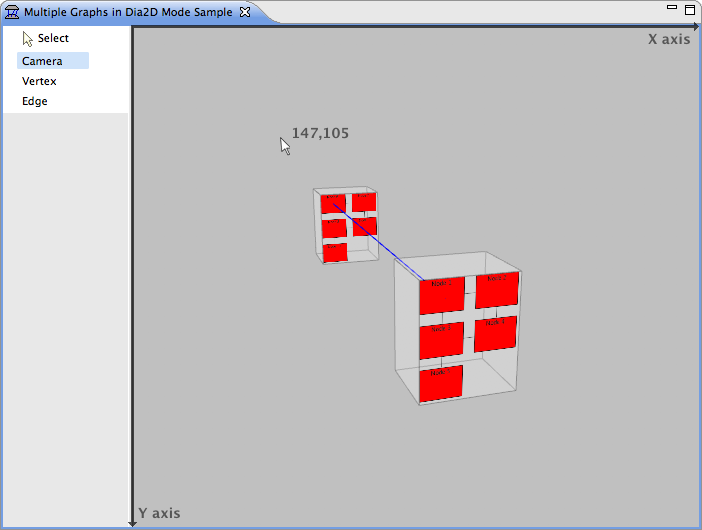
| − | + | Mouse coordinates are used to specify the location of the mouse cursor relative to a control. In the case of GEF3D, the control is the OpenGL canvas, in which the OpenGL viewport is rendered. | |
| + | |||
| + | [[Image:Mouse_coordinates.png|Mouse coordinate system]] | ||
| + | |||
| + | The origin of the mouse coordinate system is in the top left corner of the viewport, so mouse coordinates are always positive integers. In the picture, the current mouse coordinates are (147,105), and these are the same values that are contained in the mouse events that the GEF lightweight system receives and dispatches to figures and tools. In GEF3D however, these coordinates are handled a bit differently in order to allow seamless integration of embedded 2D editors (see below). | ||
| + | |||
=== World Coordinates === | === World Coordinates === | ||
3D coordinates in world space | 3D coordinates in world space | ||
| Line 9: | Line 14: | ||
origin seems to be in the upper left / front corner | origin seems to be in the upper left / front corner | ||
==== Figure-local 3D Coordinates ==== | ==== Figure-local 3D Coordinates ==== | ||
| − | === | + | === Surface Coordinates === |
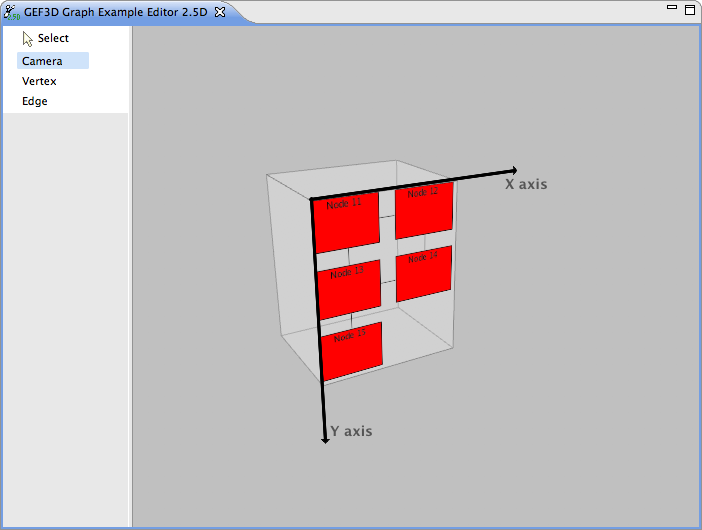
| − | 2D | + | When a GEF 2D editor is embedded in GEF3D, its content figure is added to a 3D host figure, usually a cuboid shape. The 2D figures are drawn on the front face of the cuboid, which we will call drawing surface. The following screenshot shows a cuboid host figure with five 2D nodes on its drawing surface: |
| + | |||
| + | [[Image:GEF3D_Surface_coordinates.png|Surface coordinate system]] | ||
| + | |||
| + | Since an embedded GEF editor cannot handle 3D coordinates, it must be supplied ''virtual'' surface 2D coordinates. This surface coordinate system has its origin in the upper left corner of the drawing surface as shown in the screenshot and the surface coordinates are integers which may be negative. Negative surface coordinates can be the result a coordinate conversion or when virtual picking is used (see below). | ||
== Coordinate Conversion == | == Coordinate Conversion == | ||
| + | |||
| + | === Mouse Coordinates to 3D World Coordinates === | ||
| + | Since the camera is basically a wrapper around the view and projection transformations (which transform world coordinates to window coordinates), it also offers a method that allows conversion of mouse coordinates to 3D world coordinates: | ||
| + | |||
| + | <source lang="java"> | ||
| + | /** | ||
| + | * Performs a reverse projection of the given mouse coordinates and depth | ||
| + | * value using the given model matrix. If the given model matrix is | ||
| + | * <code>null</code>, it is ignored (in other words, it is replaced with the | ||
| + | * identity matrix). The result vector contains the world coordinates of the | ||
| + | * point at the given screen coordinates and depth. | ||
| + | * | ||
| + | * @param i_xm | ||
| + | * the X mouse coordinate | ||
| + | * @param i_ym | ||
| + | * the Y mouse coordinate | ||
| + | * @param i_d | ||
| + | * the depth value | ||
| + | * @param i_modelMatrix | ||
| + | * the model matrix | ||
| + | * @param io_result | ||
| + | * the result vector, if <code>null</code>, a new vector will be | ||
| + | * created | ||
| + | * @return the result vector | ||
| + | */ | ||
| + | public IVector3f unProject(int i_xm, int i_ym, float i_d, IMatrix4f i_modelMatrix, Vector3f io_result); | ||
| + | </source> | ||
| + | |||
| + | Mouse coordinates and OpenGL window coordinates are equivalent except that the origin of the window coordinate system is in the lower left corner of the viewport, whereas the origin of the mouse coordinate system is in the upper left. This method conveniently expects mouse coordinates and handles the inversion of the Y axis itself. | ||
| + | |||
| + | === 3D World Coordinates to Mouse Coordinates === | ||
| + | The camera also supports coordinate conversion in the opposite direction: | ||
| + | |||
| + | <source lang="java"> | ||
| + | /** | ||
| + | * Performs a projection of the given world coordinates to mouse | ||
| + | * coordinates. In other words, it calculates the pixel which a ray from the | ||
| + | * eye to the given 3D point would intersect with. | ||
| + | * | ||
| + | * @param i_xw | ||
| + | * the X world coordinate | ||
| + | * @param i_yw | ||
| + | * the Y world coordinate | ||
| + | * @param i_zw | ||
| + | * the Z world coordinate | ||
| + | * @param io_result | ||
| + | * the result point, if <code>null</code>, a new point will be | ||
| + | * created | ||
| + | * @return the result point | ||
| + | */ | ||
| + | public Point project(float i_xw, float i_yw, float i_zw, Point io_result); | ||
| + | </source> | ||
| + | |||
| + | This method will calculate the mouse coordinates of a given point in 3D world coordinates. | ||
| + | |||
| + | === Surface Coordinates to 3D World Coordinates === | ||
| + | To convert surface coordinates to 3D world coordinates, a reference 3D figure is needed, which is usually the host figure of the embedded 2D editor that uses the surface coordinates. The IFigure2DHost3D interface contains two methods that allow conversion of surface to world coordinates using the implementing figure as the reference: | ||
| + | |||
| + | <source lang="java"> | ||
| + | /** | ||
| + | * Converts the given surface 2D coordinates to 3D world coordinates. | ||
| + | * | ||
| + | * @param i_sX | ||
| + | * the surface X coordinate | ||
| + | * @param i_sY | ||
| + | * the surface Y coordinate | ||
| + | * @param io_result | ||
| + | * the result vector, if <code>null</code>, a new vector will be | ||
| + | * created | ||
| + | * | ||
| + | * @return the 3D world coordinates of the given surface coordinates | ||
| + | */ | ||
| + | public IVector3f getLocation3D(int i_sX, int i_sY, Vector3f io_result); | ||
| + | |||
| + | /** | ||
| + | * Converts the given surface 2D coordinates to 3D world coordinates. | ||
| + | * | ||
| + | * @param i_sCoords | ||
| + | * the surface coordinates | ||
| + | * @param io_result | ||
| + | * the result vector, if <code>null</code>, a new vector will be | ||
| + | * created | ||
| + | * | ||
| + | * @return the 3D world coordinates of the given surface point | ||
| + | */ | ||
| + | public IVector3f getLocation3D(Point i_sCoords, Vector3f io_result); | ||
| + | </source> | ||
| + | |||
| + | The second method is a convenience method which takes a point with surface coordinates and the first method takes two integer coordinates. | ||
| + | |||
| + | === 3D World Coordinates to Surface Coordinates === | ||
| + | The same as above applies to the opposite direction: A host figure is needed as a reference, so IFigure2DHost3D contains two methods to convert 3D world coordinates to surface coordinates | ||
| + | |||
| + | <source lang="Java"> | ||
| + | /** | ||
| + | * Converts the given 3D world coordinates to 2D surface coordinates. The | ||
| + | * surface point is specified by the intersection of a line that is | ||
| + | * perpendicular to the figure's surface and that contains the given point. | ||
| + | * | ||
| + | * @param i_wX | ||
| + | * the world X coordinate | ||
| + | * @param i_wY | ||
| + | * the world Y coordinate | ||
| + | * @param i_wZ | ||
| + | * the world Z coordinate | ||
| + | * @param io_result | ||
| + | * the result point, if <code>null</code>, a new point will be | ||
| + | * created | ||
| + | * @return the 2D surface coordinates of the given 3D point | ||
| + | */ | ||
| + | public Point getLocation2D(float i_wX, float i_wY, float i_wZ, Point io_result); | ||
| + | |||
| + | /** | ||
| + | * Converts the given 3D world coordinates to 2D surface coordinates. The | ||
| + | * surface point is specified by the intersection of a line that is | ||
| + | * perpendicular to the figure's surface and that contains the given point. | ||
| + | * | ||
| + | * @param i_wCoords | ||
| + | * the 3D world coordinates | ||
| + | * @param io_result | ||
| + | * the result point, if <code>null</code>, a new point will be | ||
| + | * created | ||
| + | * @return the 2D surface coordinates of the given 3D point | ||
| + | */ | ||
| + | public Point getLocation2D(IVector3f i_wCoords, Point io_result); | ||
| + | </source> | ||
| + | |||
| + | Note that the 3D coordinates to not have to be on the host figure's drawing surface. The given 3D point is projected onto the surface before the surface coordinates are calculated. | ||
| + | |||
* global world coordinates <-> figure-local 3D coordinates | * global world coordinates <-> figure-local 3D coordinates | ||
* surface coordinates <-> global world coordinates | * surface coordinates <-> global world coordinates | ||
| Line 22: | Line 160: | ||
=== Make Yourself at Home: Creating a Fake 2D Environment === | === Make Yourself at Home: Creating a Fake 2D Environment === | ||
Coordinate conversion, Virtual picking, modified SWT events | Coordinate conversion, Virtual picking, modified SWT events | ||
| + | |||
| + | [[Category:GEF3D]] | ||
Latest revision as of 08:27, 29 December 2010
In GEF, there usually is one global coordinate system and figure-local coordinate systems to deal with. Generally, mouse coordinates can be translate to the global coordinate system and the figure-local coordinate systems in a simple and straightforward fashion, and users of the framework seldomly have to deal with these issues. In GEF3D however, there are more coordinate systems involved and dealing with those can become cumbersome. This article aims to describe the concepts of coordinate systems and coordinate system conversion in GEF3D.
Coordinate Systems
Mouse Coordinates
Mouse coordinates are used to specify the location of the mouse cursor relative to a control. In the case of GEF3D, the control is the OpenGL canvas, in which the OpenGL viewport is rendered.
The origin of the mouse coordinate system is in the top left corner of the viewport, so mouse coordinates are always positive integers. In the picture, the current mouse coordinates are (147,105), and these are the same values that are contained in the mouse events that the GEF lightweight system receives and dispatches to figures and tools. In GEF3D however, these coordinates are handled a bit differently in order to allow seamless integration of embedded 2D editors (see below).
World Coordinates
3D coordinates in world space
Inverted Coordinate System
origin seems to be in the upper left / front corner
Figure-local 3D Coordinates
Surface Coordinates
When a GEF 2D editor is embedded in GEF3D, its content figure is added to a 3D host figure, usually a cuboid shape. The 2D figures are drawn on the front face of the cuboid, which we will call drawing surface. The following screenshot shows a cuboid host figure with five 2D nodes on its drawing surface:
Since an embedded GEF editor cannot handle 3D coordinates, it must be supplied virtual surface 2D coordinates. This surface coordinate system has its origin in the upper left corner of the drawing surface as shown in the screenshot and the surface coordinates are integers which may be negative. Negative surface coordinates can be the result a coordinate conversion or when virtual picking is used (see below).
Coordinate Conversion
Mouse Coordinates to 3D World Coordinates
Since the camera is basically a wrapper around the view and projection transformations (which transform world coordinates to window coordinates), it also offers a method that allows conversion of mouse coordinates to 3D world coordinates:
/** * Performs a reverse projection of the given mouse coordinates and depth * value using the given model matrix. If the given model matrix is * <code>null</code>, it is ignored (in other words, it is replaced with the * identity matrix). The result vector contains the world coordinates of the * point at the given screen coordinates and depth. * * @param i_xm * the X mouse coordinate * @param i_ym * the Y mouse coordinate * @param i_d * the depth value * @param i_modelMatrix * the model matrix * @param io_result * the result vector, if <code>null</code>, a new vector will be * created * @return the result vector */ public IVector3f unProject(int i_xm, int i_ym, float i_d, IMatrix4f i_modelMatrix, Vector3f io_result);
Mouse coordinates and OpenGL window coordinates are equivalent except that the origin of the window coordinate system is in the lower left corner of the viewport, whereas the origin of the mouse coordinate system is in the upper left. This method conveniently expects mouse coordinates and handles the inversion of the Y axis itself.
3D World Coordinates to Mouse Coordinates
The camera also supports coordinate conversion in the opposite direction:
/** * Performs a projection of the given world coordinates to mouse * coordinates. In other words, it calculates the pixel which a ray from the * eye to the given 3D point would intersect with. * * @param i_xw * the X world coordinate * @param i_yw * the Y world coordinate * @param i_zw * the Z world coordinate * @param io_result * the result point, if <code>null</code>, a new point will be * created * @return the result point */ public Point project(float i_xw, float i_yw, float i_zw, Point io_result);
This method will calculate the mouse coordinates of a given point in 3D world coordinates.
Surface Coordinates to 3D World Coordinates
To convert surface coordinates to 3D world coordinates, a reference 3D figure is needed, which is usually the host figure of the embedded 2D editor that uses the surface coordinates. The IFigure2DHost3D interface contains two methods that allow conversion of surface to world coordinates using the implementing figure as the reference:
/** * Converts the given surface 2D coordinates to 3D world coordinates. * * @param i_sX * the surface X coordinate * @param i_sY * the surface Y coordinate * @param io_result * the result vector, if <code>null</code>, a new vector will be * created * * @return the 3D world coordinates of the given surface coordinates */ public IVector3f getLocation3D(int i_sX, int i_sY, Vector3f io_result); /** * Converts the given surface 2D coordinates to 3D world coordinates. * * @param i_sCoords * the surface coordinates * @param io_result * the result vector, if <code>null</code>, a new vector will be * created * * @return the 3D world coordinates of the given surface point */ public IVector3f getLocation3D(Point i_sCoords, Vector3f io_result);
The second method is a convenience method which takes a point with surface coordinates and the first method takes two integer coordinates.
3D World Coordinates to Surface Coordinates
The same as above applies to the opposite direction: A host figure is needed as a reference, so IFigure2DHost3D contains two methods to convert 3D world coordinates to surface coordinates
/** * Converts the given 3D world coordinates to 2D surface coordinates. The * surface point is specified by the intersection of a line that is * perpendicular to the figure's surface and that contains the given point. * * @param i_wX * the world X coordinate * @param i_wY * the world Y coordinate * @param i_wZ * the world Z coordinate * @param io_result * the result point, if <code>null</code>, a new point will be * created * @return the 2D surface coordinates of the given 3D point */ public Point getLocation2D(float i_wX, float i_wY, float i_wZ, Point io_result); /** * Converts the given 3D world coordinates to 2D surface coordinates. The * surface point is specified by the intersection of a line that is * perpendicular to the figure's surface and that contains the given point. * * @param i_wCoords * the 3D world coordinates * @param io_result * the result point, if <code>null</code>, a new point will be * created * @return the 2D surface coordinates of the given 3D point */ public Point getLocation2D(IVector3f i_wCoords, Point io_result);
Note that the 3D coordinates to not have to be on the host figure's drawing surface. The given 3D point is projected onto the surface before the surface coordinates are calculated.
- global world coordinates <-> figure-local 3D coordinates
- surface coordinates <-> global world coordinates
- screen coordinates + depth value -> global world coordinates
- screen coordinates -> figure-local 3D coordinates
- screen coordinates -> surface coordinates
Embedded 2D GEF Editors
Make Yourself at Home: Creating a Fake 2D Environment
Coordinate conversion, Virtual picking, modified SWT events