Notice: this Wiki will be going read only early in 2024 and edits will no longer be possible. Please see: https://gitlab.eclipse.org/eclipsefdn/helpdesk/-/wikis/Wiki-shutdown-plan for the plan.
Difference between revisions of "Epidemiological Parameters"
(→The Difference between the Basic Reproductive Number and the Transmission Rate) |
(→Infectious Mortality Rate (approximation)) |
||
| Line 60: | Line 60: | ||
The infectious mortality rate '''ξ''' represents the rate at which infected people die. It is ''not'' to be confused with | The infectious mortality rate '''ξ''' represents the rate at which infected people die. It is ''not'' to be confused with | ||
the net '''case fatality rate''' ('''CFR'''). | the net '''case fatality rate''' ('''CFR'''). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | If the infectious mortality rate is ''much less'' than the inverse of the period of infection | |
| + | (and we define the inverse of the period of infection as the '''recovery rate''' γ) then | ||
if: | if: | ||
ξ << γ | ξ << γ | ||
Revision as of 15:44, 24 April 2015
About Epidemiological Parameters
Common Variables and their Units
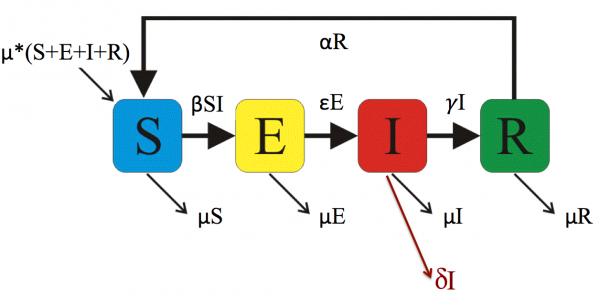
Using an SEIR model as an example lets discuss some common epidemiological parameters and what they mean. The figure shows the compartments for S=Susceptible, E=Exposed (but not yet infectious), I=Infectious (Shedding Virus), R=Recovered. The arrows show the transitions or people moving between the compartments in a specified time interval. Please also see the page Introduction to Compartment Models for more information (but please read this page first).
What they mean
The table below shows the epidemiological parameters for the SEIR model shown above. Note that the UNITS or all or the parameters are inverse time.
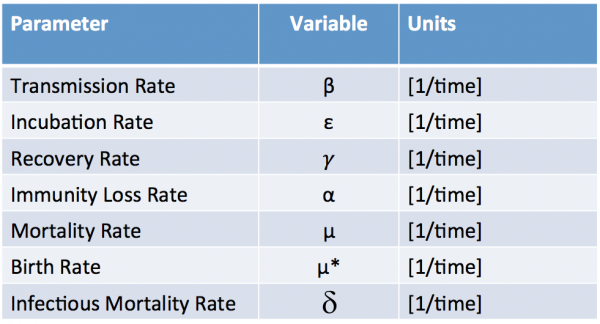 Figure 1: SEIR Compartment Model
Figure 1: SEIR Compartment Model
Each of the parameters are rate constants. The transmission rate β has a special role in that it appears inside the mass action term. This interaction term includes the product SI.
If the compartments are all normalize so that the total population S+E+I+R = 1 then Susceptible individuals become exposed at a rate, βSI For S+E+I+R = P, the rate of exposure (or the incidence) becomes βSI/P
Common Questions
All of the parameters defined above (and as used in STEM) are rate constants so their values depend on the user specified time period.
Mortality Rate
The mortality rate μ represents the rate at which individuals die even with no disease. For a constant population the mortality rate = the birth rate (or μ=μ*). For humans, if the average life span is 50 years, and if the time period is 1 day, then μ = (1/50 years) * (1 year/365.25 days) = (1/18262.5 days) or μ = 5.476 x 10-5[days-1].
Infectious Mortality Rate (approximation)
The infectious mortality rate ξ represents the rate at which infected people die. It is not to be confused with the net case fatality rate (CFR). If the infectious mortality rate is much less than the inverse of the period of infection (and we define the inverse of the period of infection as the recovery rate γ) then if: ξ << γ we can approximate the infectious mortality rate as ξ ~ CFR * γ
Infectious Mortality Rate (more generally)
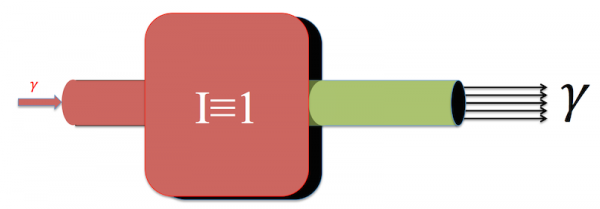
In general, for large mortality rates, this approximation is incorrect. To understand the general solution, the figures below show the flow of individuals into and out of the infectious compartment as a "pipe model".
For simplicity consider a steady state case where we always have a constant I ≡ 1. There is always then a flow in equal to the flow out. In the figure below individuals leaving the I compartment leave by only one path (into an R compartment not shown). In this simple case the inverse of the period of infection is literally the "recovery rate". The flow out (and the flow in) is γ for I ≡ 1
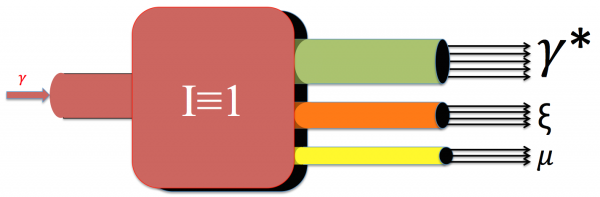
Now lets look at a case where individuals may leave the Infectious compartment by three different paths (the flow is into three pipes). They may recover (flow γ*), they may die from the disease (flow ξ), or they may die of natural causes while infectious (flow μ). If, for example, the rate of infectious mortality ξ is not very small compared to γ, then clearly we need to make a correction to the recovery rate &gamma*. The steady state figure makes this clear. By definition we always have:
γ ≡ 1/(Period of Infection)
so if we don't want the period of infection to change (i.e., if the flow out is still to add up to γ), then we need to adjust the recovery rate γ* A little algebra shows the general answer is:
γ* = γ/(γ + ξ + μ)
and the infectious mortality rate becomes:
ξ = CFR*γ/(γ + CFR + μ)
where here we keep the assumption that μ<<γ (rate if death by natural causes is much smaller than 1/period of infection).
The Difference between the Basic Reproductive Number and the Transmission Rate
A common question or confusion concerns the difference between the Basic Reproductive Number Ro and the Transmission Rate β. As discussed above, the transmission rate β, is the rate at which infectious cases cause secondary or new cases in a population, P, with S susceptible individuals. It is a rate constant and has units of inverse time (e.g., [days-1]).
The basic reproduction number , Ro, (sometimes called basic reproductive ratio) of an infection can be thought of as the number of cases one single case generates on average over the course of its infectious period, in a totaly susceptible (or otherwise uninfected) population. Ro is a dimensionless or unit-less parameter, and it is 'not a rate.
Epidemiologists want to compute or estimate Ro because;
when Ro < 1 the infection will die out in the long run. But if and when Ro > 1 the infection will spread in a population and can cause an epidemic.
The transmission rate β is an important control variable in an epidemiological model. The Basic Reproductive Number Ro can easily be calculated but it is a function of several epidemiological parameters. Conceptually (and by dimensional analysis) Ro is simply the ratio of the transmission rate (e.g. per day) divided by the recovery rate (e.g., per day).
In general Ro is the ratio of the transmission rate to the total rate at which individuals leave the infectious (I) compartment. So, if there is zero mortality,
Ro = β/γ
with a non-zero mortality rate μ
Ro = β/[γ + μ]
and with a net disease death rate ξ
Ro = β/[γ + μ + ξ]
etc. Notice that in all three cases above the numerator and denominator have the same units so Ro is dimensionless. Obviously γ , μ , ξ and β must all be provided or specified using the same time units (e.g., [days-1].